프로그래머스 - 징검다리

https://programmers.co.kr/learn/courses/30/lessons/43236

 

문제 설명

출발지점부터 distance만큼 떨어진 곳에 도착점이 있고, 그 사이에는 바위들이 놓여있다.
주어진 바위를 n개만큼 제거한다고 했을 때, 바위 사이의 최소 거리의 최댓값 값을 리턴하자.

예시는 다음과 같다.

---

바위 =  [2, 11, 14, 17, 21], n = 2, distance = 25

제거한 바위의 위치	제거 후 바위의 위치	각 바위 사이의 거리	거리의 최솟값
[21, 17]	[2,11,14]	[2, 9, 3, 11]	2
[2, 21]	[11,14,17]	[11, 3, 3, 8]	3
[2, 11]	[14,17,21]	[14, 3, 4, 4]	3
[11, 21]	[2,14,17]	[2, 12, 3, 8]	2
[2, 14]	[11,17,21]	[11, 6, 4, 4]	4

---

 

제한 사항

• 1 <= distance <= 1,000,000,000
• 1 <= 바위 수 <= 50,000
• 1 <= n <= 바위 수

 

1. Binary Search - O(NlogK)

주어진 바위 개수가 주어졌고, 제거해야 할 바위 수 n이 주어졌을 때, 가장 간단하게 생각할 수 있는 방법은 무엇이 있을까?

위의 표 처럼 - 비록 모든 경우의 수를 적은건 아니지만 - 가능한 모든 경우에 대해 바위를 치워본 후, 각 바위 사이의 거리의 최솟값을 구하면 된다.

위의 예제에서 가능한 경우의 수는 총 몇 가지일까?
5개의 바위 중에서 2개의 바위를 선택하여 치우는 경우의 수를 찾아야 한다. 따라서 5C2 = 5! / 2!3! = 10의 경우의 수에 대해 찾아보면 된다.

하지만 이 문제에서 주어지는 바위의 최대 갯수는 50,000개이다.
그리고 지워야 하는 바위의 갯수가 25,000개가 된다면 경우의 수는 어떻게 될까?

 50000! / 25000! 25000! = ??????

상상 이상의 숫자가 펼쳐질 것이다. 계산기로 25000!를 입력하면?

모든 경우의 수를 탐색하는 것은 어림도 없다는 것을 알았다.
그러면 어떻게 문제를 해결해야 할까?

 

생각을 바꿔보자. 거리의 최솟값이 될 수 있는 값의 범위는 어떻게 될까?

거리는 아무리 짧아봤자 1 미만으로 떨어질 수는 없다.
거리는 아무리 멀어져봤자 distance를 넘어설 순 없다.

즉, 정답은 1과 distance 사이에 있다고 할 수 있다. (1, distance 포함)

우선은 아무 값이나 “이 값이 바위 사이의 최솟값이 될 수 있을거야!”라고 질러보고, 그게 가능한지 확인해보자. 맞으면 맞는거고, 아니면 아닌거다. 그리고 또 다른 값을 찾아보면 될 뿐이다. 그 맞는 값들 중 최댓값을 찾으면 된다.

그러면 이 값이 최솟값이 될 수 있을지 어떻게 판별할까?

n개의 바위를 지워야 할 때, 바위 사이의 거리가 최솟값 5를 만족할 수 있는지 확인해보려 한다고 가정해보자.

모든 바위를 차례대로 순회를 하면서 각 바위 사이의 거리를 확인해보자.

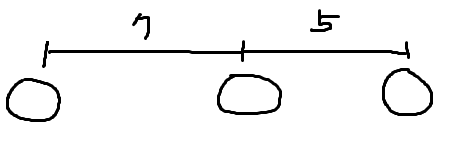
만약 지정한 값보다 바위 사이의 거리가 길다면? 이럴 때는 바위를 제거하지 않아도 괜찮다. 이 바위를 제거한다고 최솟값을 만족시키지 못하는 것은 아니기 때문이다. 이러한 바위를 지워야 할 때는 나머지 모든 바위들이 최솟값을 만족시켜서 아무 바위나 지워야 할 때 뿐이다.

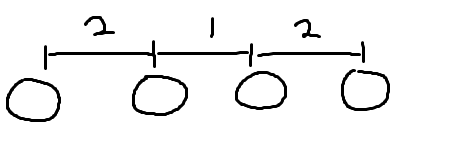
하지만 지정한 값보다 바위 사이의 거리가 좁다면? 이 경우 바위를 제거하지 않으면 주어진 조건을 만족시킬 수 없다. 지금 까지 진행해온 바위는 주어진 최솟값을 만족시키면서 왔다고 가정하고, 뒤 쪽의 바위를 제거하자.

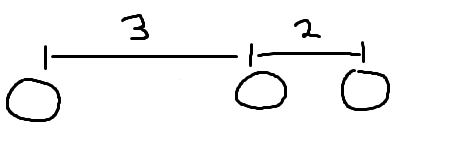
물론 지웠다고 해서 항상 조건을 만족시킬거라는 보장은 없다.
조건을 만족할 때 까지 바위를 지워주자.

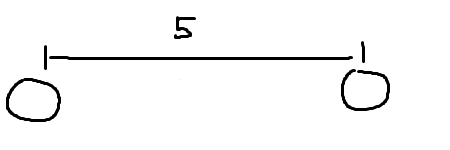
위와 같이 조건을 만족했다면 다음 바위로 넘어가자.

이 과정을 마지막 바위에 대해서까지 진행하도록 하자. 도중에 바위를 지운 횟수가 n을 초과했다면, 그 즉시 종료해도 좋다.

바위를 지워나가는 도중에, 지운 바위의 개수가 n을 초과했다면 n개의 바위를 치워서는 최소거리 5를 만족할 수 없다는 의미이고, 지운 바위의 개수가 n 이하라면 최소거리 5를 만족할 수 있다는 의미이다.

 

지워야 하는 바위 n개로 최소거리 i를 만족하는지 확인하는 방법에 대해 생각해봤으니, 이제는 i의 최댓값을 찾는 방법을 생각해야 한다.

시작지점은 0이고, 끝지점은 distance다.

하지만 distance의 최댓값은 1,000,000,000이다.
1부터 1,000,000,000까지 하나하나 다 해볼수는 없다.

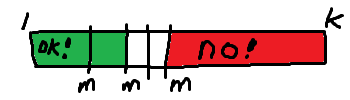
그래서 존재하는 것이 Binary Serach(이분 탐색)이다.
만약 특정 거리 l이 최소 거리가 될 수 있다면, l보다 작은 값들도 최소 거리를 만족할 수 있다. 그리고 특정 거리 r이 특정 거리를 만족할 수 없다면, r보다 큰 값들도 최소 거리를 만족할 수 없다. 따라서 이 문제에서는 이분 탐색을 사용할 수 있다.

최솟값과 최댓값의 평균이 조건을 만족할 수 있는지 확인하고, 만약에 조건을 만족할 수 있다면 최솟값을 평균 + 1로, 만족할 수 없다면 최댓값을 평균-1로 만들면서 이 과정을 반복하자.
최솟값이 최댓값을 넘어서면 이 과정을 멈추고, 최솟값 - 1을 리턴한다. 최솟값은 조건을 만족시킨 평균에 1이 더해진 값이기 때문이다.

만약 프로그래머스 - 예산을 풀어봤었다면, 익숙한 방법일 것이다.

 

그러면 이 과정을 코드로 표현해보자.

이 코드에서는 끝 지점에 바위를 하나 추가했다.
끝 지점의 바위를 지우는 행동은 기준점으로 잡은 바위를 제거하는 행위로 이해하자.

 

solution.cpp

#include <vector>
#include <algorithm>

using namespace std;

int solution(int distance, vector<int> rocks, int n) {
	int l = 1, r = distance;

	sort(rocks.begin(), rocks.end());
	rocks.push_back(distance);

	while (l <= r)
	{
		int m = (l + r) / 2, removed = 0;
		while (rocks[removed] < m)     ++removed;

		int p = removed, d = 0;

		for (int i = removed + 1; i < rocks.size(); ++i)
			if ((rocks[i] - rocks[p]) < m)
			{
				if (++removed > n)
                    break;
			}
			else
				p = i;

        if (removed <= n)   l = m + 1;
        else                r = m - 1;
	}

	return l-1;
}