프로그래머스 - 조이스틱

https://programmers.co.kr/learn/courses/30/lessons/42860

 

문제 설명

조이스틱으로 특정 알파벳 이름을 완성해야 한다.

맨 처음에는 글자가 ‘A’로만 이루어져 있다.
ex) “SNK”를 완성해야 한다고 하면, 처음에는 “AAA”이다.

• 조이스틱을 위로 올리면 다음 알파벳으로 넘어간다. (‘A’ -> ‘B’)
• 조이스틱을 밑으로 내리면 이전 알파벳으로 돌아간다. (‘B’ -> ‘A’)
  ‘A’에서 내리면 ‘Z’가 된다.
• 조이스틱을 왼쪽으로 이동하면 커서가 왼쪽으로 이동한다.
  첫 번째에서 왼쪽으로 이동하면 마지막으로 이동한다.
• 조이스틱을 오른쪽으로 이동하면 커서가 오른쪽으로 이동한다.

위의 규칙을 토대로, 조이스틱 조작 횟수의 최솟값을 리턴하자.

 

제한 사항

• 알파벳 대문자로만 이루어져있다.
• 1 <= 완성해야 하는 알파벳 길이 <= 20

 

1. 탐색? - O(N^2)

 

조이스틱을 이용하여 이름을 완성하는 과정은 다음과 같다.

• 위/아래로 움직여서 하나의 글자를 완성한다.
• 왼쪽/오른쪽으로 움직여서 다음으로 완성할 글자로 커서를 옮긴다.

위의 두 과정에서 소요되는 조이스틱의 움직임의 합이 최소가 되어야 한다.

그러면, 첫 번째로 위/아래로 움직여서 하나의 글자를 완성하는데 필요한 최소 움직임에 대해서 생각해보자.

가장 먼저 생각할 수 있는건, 조이스틱의 방향을 위로 했으면 끝까지 위로, 아래로 했으면 끝까지 아래로 움직여야 한다는 사실을 알 수 있다.

‘C’를 만들기 위해서 위 - 아래 - 위 - 위 를 하는것 보단, 위 - 위를 하는 편이 훨씬 움직임의 수가 줄어들기 때문이다. 위와 아래의 동작이 같이 들어가게 되면, 사실상 아무것도 안하는 동작이나 다를 바 없는데, 조이스틱 움직임 횟수는 2회나 늘어나버린다.

그러면 각 글자마다 움직여야 하는 최소 횟수는 정해져 있는게 아닐까?
그렇다. ‘A’는 아무것도 안해도 되니 0회, ‘B’는 위로 1회, ‘Z’는 아래로 1회 등, 각 알파벳마다 최소 횟수는 정해져있다.
따라서, 레버를 위/아래로 움직여야 하는 횟수는 항상 정해져있다.
주어진 문자열이 “AAKAA”든, “KAAAA”든, 레버를 위/아래로 움직여야 하는 횟수는 똑같다. 따라서, 각 알파벳별로 필요한 움직임 횟수를 구하는 함수를 따로 작성해도 괜찮지만, 아예 배열에 미리 계산한 값을 집어넣는 방법도 있다. 편한대로 하자.

그러면 남은 부분은 조이스틱을 좌/우로 움직임에 대한 최솟값을 구해야 한다.

좌/우 움직임의 최댓값은 몇일까? 적어도 이름 길이-1을 넘어서지는 못할 것이다. 한 쪽 방향으로만 쭉 가는 경우, 좌/우 움직임을 이름 길이-1번을 해야하기 때문이다.

"EEE"를 만들기 위해 필요한 좌/우 움직임은 2고,
"EEEEEEE"를 만들기 위해 필요한 좌/우 움직임은 6이다.

그러면 어떤 상황에서 이름 길이-1보다 적은 움직임으로 완성할 수 있을까?

맨 처음에 주어지는 문자열은 모두 'A'로 초기화가 되어 있다. 그래서 'A'는 내버려둬도 이미 완성되어 있는 글자다.

따라서, "DKAAAAAA"를 완성하기 위해서는 좌/우 이동을 오른쪽으로 딱 한번만 하면 된다. 나머지 "AAAAAA"는 이미 완성이 되어있기 때문이다.

이번엔 조금 더 생각을 해야 하는 경우를 확인해보자.
"BBBAAAAAAAAB"는 몇 번의 좌/우 움직임이 필요할까? 직관적으로 생각해보면, 왼쪽으로 한 번 가서 맨 끝의 'B'를 완성한 후, 오른쪽으로 계속 이동하면서 나머지 "BBB"를 완성하는 편이 짧아 보이고, 실제로도 그렇다. 단 4번의 좌/우 움직임만을 필요로 한다.

"BBAAAAAAAABB"의 경우도 마찬가지다. 단지 이번에는 오른쪽으로 1번, 그리고 왼쪽으로 3번을 움직여야 할 뿐이다.

하지만 "BBBBBBBAABB"의 경우는 다르다. 도중에 한 번 꺾느니 차라리 한 방향으로 쭉 가야 움직임을 최소화 할 수 있다. 그러면 꺾어야 하는 판단은 어떻게 해야 할까?

 

"BBBAAAAAAAAB"를 보면서 생각해보자.

오른쪽으로 한 칸 이동한 뒤 방향을 꺾으면 얼마나 더 가야할까?
이름 길이 - 1 만큼 이동해야 한다. 바로 옆에 'B'가 있기 때문이다.

오른쪽으로 두 칸 이동한 뒤 방향을 꺾으면 얼마나 더 가야할까?
딱 세 칸만 더 이동하면 된다. 그러면 총 2 + 3 = 5번의 이동으로 끝낼 수 있다. 즉, 우우좌좌좌 로 이동하는 것이다.

그런데, 여기서 순서를 반대로 하면 어떨까?
왼쪽으로 한 칸 이동한 뒤 오른쪽으로 쭉 이동하면? 1 + 3 = 4번의 이동으로 끝낼 수 있다. 오른쪽 -> 왼쪽 보다 1번의 이동을 절약할 수 있다. 즉, 좌우우우로 이동하는 것이다.

이 과정을 자세히 보면, 왼쪽 1번, 그리고 오른쪽 2번은 반드시 포함되어 있는 것을 알 수 있다. 차이점은 전자는 왼쪽이 2번이고, 후자는 오른쪽이 1번이다.

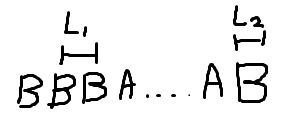
위의 그림에서 볼 수 있듯이, 최소한 L1 + L2번 만큼은 이동을 해야 한다는 사실을 알 수 있다. 그리고 L1번을 먼저 이동했다면 다시 한 번 L1번을 이동하여 시작지점으로 돌아온 뒤 L2번을 이동해야 하고, L2번을 먼저 이동했다면, 다사 한 번 L2번을 이동하여 시작지점으로 돌아온 뒤, L1번을 이동해야 한다는 사실을 알 수 있다. 따라서, L1이나 L2중 짧은 쪽을 먼저 이동한 뒤, 다시 한 번 이동하여 시작지점으로 돌아온 뒤, 마지막으로 L1이나 L2중 이동하지 않았던 곳을 이동하여 마무리 하면 좌/우 이동의 최솟값을 구할 수 있을 것이다.

그러면 L2의 시작점은 어떻게 잡을까?
L1의 끝 점에서 'A' 가 아닌 글자를 처음 만나는 지점이 L2의 시작점이다. L1의 끝 점에서 방향을 틀거나 오른쪽 이동을 끝냈을 때, L2의 시작점에 있는 글자도 'A'가 아닌 다른 글자로 맞춰야 비로소 이름이 완성되기 때문이다.

이를 수식화 하면 다음과 같다.
만들어야 하는 이름의 길이를 L이라고 하고,
L1의 끝 점을 t, L2의 시작점을 p라고 하자.

t + (L-p) + min(t, (L-p))

그러면 이 값의 최소가 되는 지점을 찾아야 하므로, 모든 지점에서 위의 식을 계산을 해 나가면 될 것이다. 순회하는 김에 위/아래 조이스틱 횟수도 더해나가면 하나의 반복문에서 모든 것을 해결할 수 있을 것이다.

그리고 아예 좌/우로 꺾지 않는다는 선택지도 있으므로, 좌/우 이동의 기본값은 이름 길이 - 1로 초기화하자.

 

그러면 이를 코드로 표현해보자.

 

solution.cpp

#include <string>

using namespace std;

int solution(string name) {
    int sc[] = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,12,11,10,9,8,7,6,5,4,3,2,1};
    int l = static_cast<int>(name.size());
    int ans = 0, t = l-1;
    
    for (int i=0;i<l;++i)
    {
        ans += sc[name[i]-'A'];
        int next = i+1;
        while ((next < l) && (name[next] == 'A'))
            ++next;
        
        t = min(t, i+l-next+min(i,l-next));
    }
    
    return ans + t;
}

 

개인적으로는 2레벨 치고는 까다로운 문제라고 생각한다.