프로그래머스 - 정수 삼각형

https://programmers.co.kr/learn/courses/30/lessons/43105

 

문제 설명

삼각형의 꼭대기에서 바닥으로 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 한다. (그림은 프로그래머스 사이트에서 보도록 하자)

아래 칸으로 이동할 때는 대각선 방향으로 왼쪽 또는 오른쪽으로 한 칸만 이동이 가능하다.
ex) 3번째 줄의 8은 2 또는 7로만 이동이 가능하다.

삼각형의 정보가 담긴 triangle 배열을 토대로, 거쳐간 숫자의 최댓값을 리턴하자.

 

제한 사항

• 1 <= len(triangle) <= 500
• 0 <= triangle[i][j] <= 9,999  

1. DFS - O(2^N) - 시간초과

문제를 풀기에 앞서, 주어진 배열에서 좌/우 이동을 어떻게 해야 할 지 생각을 해 볼 필요가 있다. 그러면 삼각형을 배열에 맞춰서 그림으로 보자.

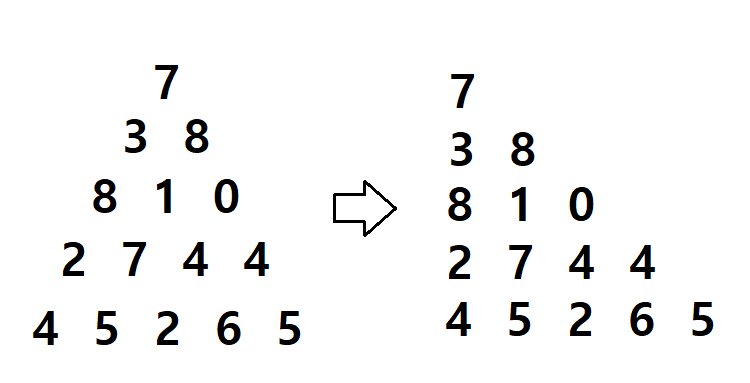
가만 보니, 삼각형의 맨 왼쪽에 있던 값은 triangle[i][0]으로 표현할 수 있고, 맨 오른쪽에 있던 값은 triangle[i][i]로 표현할 수 있음을 알 수 있다.
그리고 삼각형의 좌표 (i,j)에서 왼쪽으로 가는 행동은 (i+1, j)로 표현할 수 있고, 오른쪽으로 가는 행동은 (i+1, j+1)로 표현할 수 있다는 것을 확인할 수 있다.

그러면 실제로 맨 꼭대기에서부터 차례대로 내려가며, 최대로 큰 경로를 찾아볼 방법을 생각해보자.

우선은 단순하게 dfs로 풀어보자.
dfs 함수의 리턴 값은 해당 경로로 갔을 때의 최댓값 을 리턴하도록 하자. 즉, dfs(0,0)은 답을 리턴하게 된다.

현재 탐색중인 정점을 (x,y)로 표현해보자. (x는 삼각형의 세로 좌표 값, y는 삼각형의 가로 좌표 값)
현재 정점의 값은 triangle[x][y]로 얻어올 수 있다. 그러면 왼쪽으로 갔을 때의 경로 값은 dfs(x+1,y)가 되고, 오른쪽으로 갔을 때의 경로 값은 dfs(x+1,y+1)이 된다. 그러면 dfs(x,y)의 값은 다음과 같이 표현할 수 있을 것이다.

triangle[x][y] + max(dfs(x+1,y), dfs(x+1,y+1))

얼마나 간단한가! 여기서 x가 삼각형의 높이를 초과하지 않도록 처리하는 코드만 추가하면, 다음과 같은 간단한 코드로 답을 구할 수 있을 것이다.

 

solution_dfs.cpp

#include <vector>

using namespace std;

int dfs(int x, int y, vector<vector<int>>& triangle)
{
    if (x >= static_cast<int>(triangle.size()))
        return 0;
    
    return triangle[x][y] + max(dfs(x+1,y,triangle), dfs(x+1,y+1,triangle));
}

int solution(vector<vector<int>> triangle) {
    return dfs(0,0,triangle);
}

 

예제를 돌려보면 잘 동작한다.
하지만 이 코드를 제출하면 이렇게 된다.

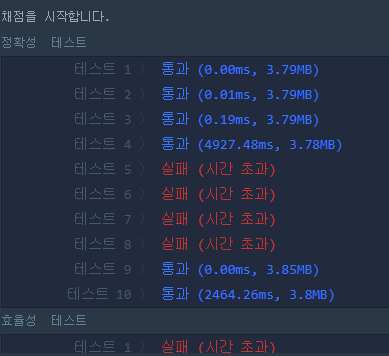
효율성 테스트도 아니고 무려 정확도 테스트에서 시간초과가 발생하고 있다. 그나마 통과한 일부 테스트 케이스도 4000ms와 2400ms가 보인다. 밑의 효율성 테스트는 볼 필요도 없이 모두 시간 초과가 발생했다.

왜 이렇게 시간이 오래 걸리는걸까? 원인은 중복계산이다.

얼마만큼의 중복계산이 발생했는지 다음 코드를 통해 알아보자.

check.cpp

#include <vector>

using namespace std;

int dfs(int x, int y, vector<vector<int>>& triangle, vector<vector<int>>& visited)
{
	if (x >= triangle.size() || y >= triangle[x].size())
		return 0;

	++visited[x][y];
	return triangle[x][y] +
		max(dfs(x + 1, y, triangle, visited), dfs(x + 1, y + 1, triangle, visited));
}

int solution(vector<vector<int>> triangle) {
	vector<vector<int>> visited(triangle.size(),
	vector<int>(triangle.size(), 0));

	int answer = dfs(0, 0, triangle, visited);

	for (int i = 0; i < static_cast<int>(triangle.size()); ++i)
	{
		for (int j = 0; j <= i; ++j)
		{
			cout << visited[i][j] << " ";
		}
		cout << endl;
	}

	return answer;
}

 

위의 코드에 기본 샘플 테스트 케이스를 집어넣으면 다음과 같이 출력될 것이다.

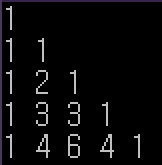
위의 그림에서 출력된 숫자의 의미는 무엇일까?
triangle[x][y] + max(dfs(x+1,y), dfs(x+1,y+1))을 수행한 횟수를 의미한다.
즉, 중복계산한 횟수가 저만큼이나 된다는 이야기이다.

그리고 각 행의 값을 더해보면, 2의 제곱수임을 알 수 있다. (1,2,4,8,…)
이는 삼각형의 높이가 1씩 추가될 때 마다 실행시간이 두 배로 증가한다는 것을 의미한다. 뭔가 효율적인 방법을 찾아야 한다.

 

2. DP - O(N^2)

위의 DFS 방식에서 문제가 되는 것은 중복계산이라고 했다. 그러면 중복계산을 방지하면 문제를 해결할 수 있을 것이다.

다음과 같이 dfs(x,y)의 결과를 담아두는 배열 d를 만들자. 초기 값은 dfs()의 결과로 생길 수 없는 값인 음수로 초기화하자. (삼각형의 값은 모두 0 이상의 값이다)

d[x][y] = -1

그 다음, 기존 코드와 동일하게 dfs(x,y)를 작성하자. 그리고 triangle[x][y] + max(...) 코드를 실행하기 전에, d[x][y]의 값이 -1인지 확인하자.

만약 -1이라면, 아직 dfs(x,y)를 계산한 적이 없다는 의미이다. 그러므로 triangle[x][y] + max(...) 코드를 실행하자. 그리고 그 결과를 d[x][y]에 집어넣자.

d[x][y] = triangle[x][y] + max(dfs(x+1,y), dfs(x+1,y+1))

만약 -1이 아니라면, 이미 dfs(x,y)를 계산한 적이 있다는 의미이다. 따라서 이 때는 굳이 triangle[x][y] + max(...)를 수행하지 않고, 이미 계산해둔 값, d[x][y]의 값을 리턴하자. 그러면 또 다시 한 번 계산했었던 dfs(x+1,y)와 dfs(x+1,y+1)을 또 다시 수행할 일이 없어진다.

그러면 위의 과정을 추가한 코드를 작성해보자.

 

solution_memoization.cpp

#include <vector>

using namespace std;

int dfs(int x, int y, vector<vector<int>>& triangle, vector<vector<int>>& d)
{
    if (x >= static_cast<int>(triangle.size()))
        return 0;
    
    return d[x][y] = (-1 == d[x][y]) ?
        triangle[x][y] + max(dfs(x+1,y,triangle,d), dfs(x+1,y+1,triangle,d)) :
        d[x][y];
}

int solution(vector<vector<int>> triangle) {
    vector<vector<int>> d(triangle.size(), vector<int>(triangle.size(), -1));
    return dfs(0,0,triangle,d);
}

 

위와 같이 이미 한 번 계산했던 값이 또 다시 필요할 경우, 기억해뒀던 값을 재활용하는 방법도 있지만, 점화식을 통해서 이전에 계산한 값을 토대로 새로운 값을 계산해내는 방식도 존재한다.

맨 위의 triangle[0][0]에서부터 triangle[x][y]까지 내려왔다고 하자. 그러면 이 때 까지 진행한 경로 중, triangle[x][y] 에 도달했을 때의 최댓값을 계산할 수 있는 방법은 무엇일까?

triangle[x][y]까지 진행했을 때의 최댓값을 표현하는 d 배열을 만들어보자. 그러면 d[x][y]는 어떻게 표현할 수 있을까?

(x,y)에 도달하기 위해선 어디를 거쳐야 할까?
(x-1,y-1)과 (x-1,y)외에는 도달할 수 있는 길이 없다. 즉, 왼쪽 위에서 오거나오른쪽 위에서 오는 방법 밖에 없다. 그러면 (x-1,y-1)까지 진행했을 때의 최댓값과 (x-1,y)까지 진행했을 때의 최댓값 중 하나를 고른 뒤, triangle[x][y]의 값을 더해주면 그 값이 d[x][y]가 될 것이다. 따라서, d[x][y]는 다음과 같이 표현할 수 있을 것이다.

d[x][y] = triangle[x][y] + max(d[x-1][y-1], d[x-1][y])

다만 여기서는 주의해야 할 점이 있는데, y의 값이 배열의 범위를 벗어날 수 있다는 점이다. 따라서 예외처리를 하는 코드를 반드시 추가하자.

위의 식을 triangle[0][0]부터 차근차근 계산해 나간 뒤, triangle[h][i]의 값들중 최댓값을 고르면 될 것이다. (h는 삼각형의 높이, i는 삼각형의 맨 밑에 올 수 있는 수)

그럼 이를 코드로 표현해보자.

solution_dp.cpp

#include <vector>
#include <algorithm>

using namespace std;
int solution(vector<vector<int>> triangle) {
    int l = static_cast<int>(triangle.size());
    vector<vector<int>> d(l, vector<int>(l, 0));
    d[0][0] = triangle[0][0];
    
    for (int i=1;i<l;++i)
    {
        d[i][0] = triangle[i][0] + d[i-1][0];
        d[i][i] = triangle[i][i] + d[i-1][i-1];
        
        for (int j=1;j<i;++j)
            d[i][j] = triangle[i][j] + max(d[i-1][j-1], d[i-1][j]);
    }
    
    return *max_element(d[l-1].begin(), d[l-1].end());
}

 

재귀를 쓰지 않아도 생각보다 간결한 코드로 표현이 가능하다.

 

---

 

위의 풀이에서의 메모리 사용량은 O(N^2)지만, 이 과정을 O(N)의 메모리 크기로도 풀 수도 있다. 기억해둔 정보는 바로 이전 단계만 사용한다는 점을 생각하면 다음과 같이 사용하는 메모리를 절약할 수 있다.

 

solution_dp_N_memory.cpp

#include <vector>
#include <algorithm>

using namespace std;

int solution(vector<vector<int>> triangle) {
    int s = triangle.size();
    vector<int> d(s,0);
    d[0] = triangle[0][0];
    
    for (int i=1;i<s;++i)
    {
        d[i] = d[i-1] + triangle[i][i];
        for (int j=i-1;j>0;--j)
            d[j] = max(d[j], d[j-1]) + triangle[i][j];
        d[0] += triangle[i][0];
    }
    
    return *max_element(d.begin(), d.end());
}