프로그래머스 - 입국심사

https://programmers.co.kr/learn/courses/30/lessons/43238

 

문제 설명

n명이 입국 심사를 위해 줄을 서서 기다리고 있다. 각각의 입국심사대에 있는 심사관마다 심사하는데 소요되는 시간이 다르다.

처음에는 모든 심사대가 비어있다. 한 심사대에서는 한 명씩만 심사를 할 수 있다. 그리고 가장 앞에 있는 사람은 비어있는 심사대로 가서 심사를 받을 수도 있다. 하지만 다른 심사관의 심사를 기다렸다가 받는 편이 더 빠를 경우, 기다렸다가 심사를 받을 수도 있다.

모든 사람이 심사를 받는 데 걸리는 시간을 최소화 하고 싶다.

입국심사를 기다리는 사람의 수를 n, 각 심사관마다 심사에 소요되는 시간을 담은 배열 times가 주어졌을 때, 모든 사람이 심사를 받는데 소요되는 시간의 최솟값을 리턴하자.

 

제한 사항

• 1 <= n <= 1,000,000,000
• 1 <= times[i] <= 1,000,000,000
• 1 <= len(times) <= 100,000

 

1. Binary Search - O(NlogK)

예시를 한 번 살펴보자.

n = 6, times = [7,10]

위의 경우 최소의 경우의 수는 어떻게 될까? 잘 모르겠으면 우선 차근차근 한 명씩 넣어보자.

맨 처음에는 두 심사대 모두 비어있으므로 0번 심사대와 1번 심사대에 보내자. 그러면 7분 후 0번 심사관이 빌 것이다.

0번 심사대에 한명을 더 보내자. 지금까지 소요된 시간은 7분, 그리고 심사가 끝난 사람은 1명이다.

3분 후 1번 심사대가 빌 것이다. 그러면 1번 심사대에 한명을 더 보낸다. 그러면 10분 소요에 심사는 2명이 끝난다.

…

이를 반복하다보면 20분째에 또 한명이 심사를 마치고, 총 4명의 사람이 심사를 마치게 된다. 그리고 마지막으로 기다리던 사람이 심사를 받으러 갈 수 있게 된다. 그런데 여기서 자리가 빈 1번 심사대로 가는 것보다 1분 후에 심사가 끝나게 될 0번 심사대를 기다리는 것이 더 좋다. 따라서 21분째에 5명의 심사가 끝나게 되고, 마지막 남은 사람이 0번 심사대로 가면 28분에 모든 심사가 끝나게 된다.

 

위의 방법에서는 한 명씩 심사대에 보내는 방식으로 풀었다. 하지만 이번 문제에서 심사를 기다리는 사람의 수는 1,000,000,000명이다. 이 많은 사람들을 한 명씩 심사대에 보내는 행동을 한다면? 당연하게도 시간 초과가 발생할 것이다. 심사대에 보내는 동작이 O(1)이라면 좋겠지만, 걸리는 시간에 따라 어느 심사대에 보낼 지에 대해서도 생각해야 한다. O(1)로는 끝날 것 같지 않아 보인다. 그러면 어떻게 풀어야 할 까?

 

다행스럽게도 이 문제의 카테고리가 힌트를 주고 있다. 이 문제의 카테고리는 이분 탐색(Binary Search)다. 카테고리에서 시키는 대로 이분 탐색을 사용하면 될 것 같다. 그러면 어떻게 이분 탐색을 수행해야 할까?

위의 문제에서 가능한 최대 소요시간은 어떻게 될까? 가장 오래 걸리는 사람에게 모두 몰아넣으면 최대 소요시간이 될 것이다.
그러면 가능한 최소 소요시간은 어떻게 될 까? 잘은 모르겠지만 1보다 작지는 않을 것이다. 가장 적게 걸리는 사람의 시간으로 해도 무방할 것이다.

그리고 정답은 최대 소요시간과 최소 소요시간의 사이에 있을 것이다.

한번 위의 예시를 이분 탐색으로 풀어보자.

 

우선 최대 소요시간과 최소 소요시간의 평균의 시간으로 모든 사람이 검문을 받을 수 있는지 확인해보자. 위의 예시에서 최대 소요시간은 60분일 것이고, 최소 소요시간은 1분일 것이므로, (60+1)/2 = 30분이 평균 시간이다.

30분동안 0번 검문소에서는 몇 명을 검문할 수 있을까? 30 / 7 = 4.28…이므로 4명을 검문할 수 있다. 28분동안 4명을 검문하면 2분이 남으므로, 2분동안은 검문을 끝낼 수 없다.
30분동안 1번 검문소에서는 몇 명을 검문할 수 있을까? 30 / 10 = 3이므로 3명을 검문할 수 있다.

그러면 30분동안 검문할 수 있는 사람의 수는 4+3 = 7이므로 6명을 검문하는데 충분한 시간이다.
그리고 이는 30분 이상의 시간이 주어지면 6명을 검문하는데 충분한 시간이다라는 것을 의미한다. 31분이 주어져도 6명을 검문할 수 있고, 40분이 주어져도 6명을 검문할 수 있다.

하지만 아직 1분에서 29분 사이의 값이 주어졌을 때의 결과는 알지 못한다. 따라서 이번엔 최댓값을 29분으로 잡고, 또 다시 평균을 내 보자. 그러면 평균은 (1+29)/2 = 15분이 된다. 15분동안은 얼마나 검문할 수 있는지 확인해보자.

15분동안 0번 검문소에서는 몇 명을 검문할 수 있을까? 15/7 = 2.14…이므로 2명을 검문할 수 있다.
15분동안 1번 검문소에서는 몇 명을 검문할 수 있을까? 15/10 = 1.5이므로 1명을 검문할 수 있다.

15분동안 검문할 수 있는 사람의 수는 2+1 = 3이므로 6명을 검문하는데 충분하지 않은 시간이다.
그리고 이는 15분 이하의 시간이 주어지면, 6명을 검문하는데 충분하지 않은 시간이다라는 것을 의미한다. 10분이 주어져도, 5분이 주어져도 6명을 검문할 수 없다는 것을 의미한다.

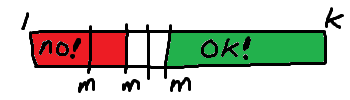
즉, 위의 이미지처럼 가장 적절한 값을 반씩 나눠가며 범위를 좁혀나가는 것이 핵심이다. 반으로 나누다보면 언젠간 끝이 오게 된다. 그리고 28분이라는 값에 도달하게 될 것이다.

 

그러면 위의 내용을 코드로 표현해보자.

값이 매우 커질 수 있으므로, 최대한 큰 값을 담을 수 있는 정수형을 사용하도록 하자.

 

solution.cpp

#include <vector>
#include <algorithm>

using namespace std;

long long solution(int n, vector<int> times) {
    long long mx = static_cast<long long>(*max_element(times.begin(), times.end()));
    long long l = 1, r = static_cast<long long>(n) * mx;
    long long answer = r;

    while (l <= r)
    {
        long long target = (l + r) / 2;
        long long cnt = 0;
        
        for (int v : times)
            cnt += target / static_cast<long long>(v);

        if (cnt >= n)   r = target - 1;
        else            l = target + 1;
    }

    return r+1;
}

 

이전에 프로그래머스 - 예산을 푼 적이 있다면, 거의 동일한 방식이라는 것을 알 수 있다. 예산은 최댓값을 찾는 문제였다면, 이번에는 최솟값을 찾는 문제라는 점이 차이라면 차이일 것이다.

나중에 프로그래머스 - 징검다리 문제를 풀게 된다 하더라도, 이와 비슷한 방법으로 풀 수 있으니, 잘 기억해두자.