프로그래머스 - 예산(이분 탐색)
https://programmers.co.kr/learn/courses/30/lessons/43237
문제 설명
하나의 국가가 있고, 그 국가에 여러 지방이 예산 요청을 하고 있다.
예산의 총액은 정해져 있고, 지방에서 요청하는 대로 배정하는게 어려울 수도 있다.
따라서, 정해진 총액 이하에서 가능한 한 최대의 예산을 배정하려 한다.
- 모든 요청에 따라 배정할 수 있으면 그대로 배정해준다.
- 모든 요청에 따라 배정할 수 없으면, 특정한 정수의 상한액을 계산하여,
그 이상인 예산 요청에는 모두 상한선에 따라 배정한다.
상한액 이하의 예산 요청에는 요청한 금액 그대로를 배정한다.
예산 총액과 각 지방의 요청 예산을 토대로, 위의 조건을 모두 만족하는 최대 예산 상한액을 리턴하자.
제한 사항
- 3 <= 지방의 수 <= 100,000
- 1 <= 지방에서 요청한 예산 <= 100,000
- 지방의 수 <= 총 예산 <= 1,000,000,000
1. 정렬 후 순회- O(NlogN)
주어진 예시를 보면서 생각해보자.
[120, 110, 140, 150], 485
주어진 예산은 485인데, 지방에서 요청하고 있는 예산의 총 합은
120 + 110 + 140 + 150 = 520이다. 따라서, 모든 지방의 요청을
들어 줄 수 없는 상황이다.
문제에 따르면, 특수한 정수의 상한을 두어, 상한선 까지만 예산을 배정한다고 되어 있다. 그리고 상한 이하의 예산에는 요청한 대로 준다고 한다.
이렇게 되면, 가장 많이 요구한 지방의 예산부터 깎이게 된다.
상한 예산을 145로 조정하게 되면, 150을 요청한 지방만 145를
받게 되기 때문이다.
그러면 가장 많이 요구한 예산부터 차례대로 깎아보자.
예산의 상한을 140으로 설정하면 어떻게 될까?
120은 140 이하이므로 그대로 받을 수 있다.
110은 140 이하이므로 그대로 받을 수 있다.
140은 140 이하이므로 그대로 받을 수 있다.
150은 140을 초과하므로 140만 받을 수 있다.
따라서, 상한을 140으로 정하면 120 + 110 + 140 + 140 = 510
의 예산이 필요하게 된다. 하지만 아직도 485를 넘는다.
그러면 이번엔 상한을 120으로 깎아보자.
위와 같은 방식으로 총 예산을 더해보면,
120 + 110 + 120 + 120 = 470이 된다. 이는 485보다 적은 수치이므로,
최대 상한 값을 120으로 설정하면 주어진 예산에 맞게 분배할 수 있다.
하지만 우리는 최대 예산 상한액을 찾고 있다. 120이 정말로 최대일까?
주어진 총 예산 485중에서 470을 쓰는 것이 정말로 최선일까?
아니다. 예산 상한을 좀 더 늘릴 수 있다. 남는 15를 좀 더 나눠줄 수 있다.
그럼 상한액을 125로 늘이면 어떻게 될까?
120 + 110 + 125 + 125 = 480으로 모든 지방에 예산을 지원할 수 있다.
그래도 아직 5가 남는다.
상한액을 127까지 늘이면, 120 + 110 + 127 + 127 = 484로
모든 지방에 예산을 배정할 수 있고, 여기서 1을 더 올린 128로 늘이면
120 + 110 + 128 + 128 = 486으로 배분이 불가능해진다.
따라서, 이 예시에서의 최대 예산 상한액은 127이다.
그렇다면 이 과정을 어떻게 하면 좀 더 간소화 시킬 수 있을까?
가장 많이 요청한 예산부터 삭감한다는 아이디어를 활용해보자.
이번에는 아예 가장 많이 요청한 예산 하나를 싹 다 빼보자. 그러면 예산의 여유가 얼마나 남을까?
485 - (120 + 110 + 140) = 115 만큼의 예산의 여유가 남았다.
이 115를 이용해서는 140 이상의 예산 상한을 설정할 수 없다.
그렇다는 것은, 예산 상한은 140을 넘길 수 없다는 것을 의미한다.
그러면 그 다음으로 많이 요청한 예산도 하나 빼 보자. 그러면 예산의 여유가 얼마나 남을까?
485 - (120 + 110) = 255의 예산이 남는다.
이 남은 255의 예산을 나머지 두 지방에 분배하면 127이다.
그리고 127은 그 다음으로 큰 예산인 120 이상이다.
그러면 가능한 최대 예산 상한액은 127이 된다.
위의 과정을 일반화 하면 다음과 같다.
- 모든 지방의 예산의 합이 가능한 예산보다 작을 경우, 지방에서 요청한 최대 예산을 리턴한다.
- 만약 그렇지 않으면, 지방에서 요청한 예산의 총량을 구한 후, 다음 과정을 반복하자.
i번째로 큰 예산을 총량에서 뺀다.- (예산 총액 - 총량) / i 를 한 값이
i-1보다 크거나 같은지 확인한다. - 크거나 같으면, 위의 값을 리턴한다.
- 이 과정을 2번째로 적게 요청한 지방에 대해서 까지만 수행한다.
- 만족하는 값을 찾지 못했으면, 예산 총액 / 지방의 수 값을 리턴한다.
그러면 이 과정을 코드로 표현해보자.
solution_sort.cpp
#include <vector>
#include <algorithm>
#include <numeric>
using namespace std;
int solution2(vector<int> budgets, int M) {
long long l = static_cast<long long>(budgets.size());
long long sum = accumulate(budgets.begin(), budgets.end(), static_cast<long long>(0));
sort(budgets.begin(), budgets.end());
if (sum <= static_cast<long long>(M))
return budgets.back();
for (long long i = l - 1; i > 0; --i)
{
sum -= static_cast<long long>(budgets[i]);
long long v = (static_cast<long long>(M) - sum) / (l - i);
if (v >= budgets[i - 1])
return static_cast<int>(v);
}
return M / static_cast<int>(l);
}
위의 코드를 확인해보면, long long으로 형변환을 하고 있는 것을 볼 수 있다.
최대로 나올 수 있는 지방의 수는 100,000이고, 각 지방의 최대 예산은
100,000이다. 100,000 * 100,000 = 10,000,000,000이다. 그리고 이 값은
int의 범위를 넘어서는 값이다. Python이라면 신경 쓸 필요는 없으나,
Java와 C++이라면 오버플로우에도 신경을 써야 한다.
사실 형변환을 하지 않아도 프로그래머스의 테스트는 통과할 수 있다.
하지만 데이터 형을 정할 때는 항상 오버플로우를 염두해 두자.
2. 이분 탐색 - O(NlogK)
정렬로도 풀 수 있지만, 이 문제의 카테고리는 이분 탐색(Binary Search)다. 이분 탐색을 어떻게 사용해야 할까?
먼저, 이 문제의 답이 될 수 있는 범위를 생각해보자.
최댓값은 지방에서 요청한 예산 중 가장 큰 값이다. 모든 요청이 배정될 수 있을 경우
요청한 금액을 그대로 배정하기 때문이다.
최솟값은 1이다. 문제에서 주어지는 총 예산의 최솟값은 지방의 수이기 때문이다.
5개의 지방이 있는데 총 예산이 5라면, 지방에서 요청한 액수와는 상관없이
각 지방마다 1밖에 줄 수 없다. 따라서 최솟값은 1이다.
즉, 답은 1과 지방에서 요청한 예산 중 가장 큰 값을 포함한 범위 안에 있다는 것을 의미한다.
그러면 1과 최댓값을 더한 값을 반으로 나눈 값(m이라고 하자) 을 최대 예산 상한액으로 가정하자. 그리고 이 값을 최대 예산 상한액으로 했을 때, 모든 지방에 예산이 분배가 가능한지 확인을 해 보았다고 치자.
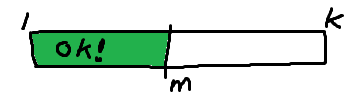
만약 모든 지방에 예산 분배가 가능했다면, m보다 작거나 같은 값을 최대 예산 상한액으로 설정했을때도 모두 분배가 가능할 것이다. 최대 예산 상한액이 줄어들면 줄어들 수록 필요한 예산은 적어지거나 같아지기 때문이다.
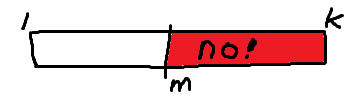
만약 모든 지방에 예산 분배가 불가능했다면, m보다 크거나 같은 값을 최대 예산 상한액으로 설정했을때도 모두 분배가 불가능할 것이다. m으로도 예산을 분배하지 못하는데, m보다 커지면 더더욱 필요한 예산이 커지거나 같아지기 때문이다.
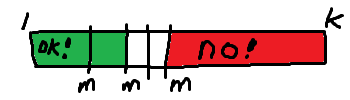
위의 과정을 통해, 우리는 절반 정도의 값에 대해 이 값으로 예산 분배 가능 여부를 확인할 수 있었다. 하지만 남은 절반은 아직 알 수 없는 상태이다. 그러면 남은 절반에 대해서도 동일한 방법으로 계속해서 절반씩 확인을 해 나갈 수 있을 것이다. 위의 그림처럼 말이다.
범위를 계속해서 절반씩만 줄이면 마치 제논의 역설처럼 끝나지 않을 것처럼 느낄 수도 있지만, 예산은 실수가 아닌 정수로 주어진다. 따라서 끝은 존재한다.
그러면 예시를 이분 탐색을 이용하여 한 번 풀어보자.
가능한 상한의 최솟값은 1이고, 최댓값은 150이다.
(1 + 150) / 2 = 75.5이니, 상한을 75로 잡았을 때 가능한지 확인해보면,
75 + 75 + 75 + 75 = 300으로 배분이 가능하다. 따라서 최댓값은 75 이상이다.
이번에는 76과 150사이의 값인 113에 대해 확인해보자.
113 + 110 + 113 + 113 = 449로 배분이 가능하다. 따라서 최댓값은 113 이상이다.
이번에는 114와 150 사이의 값인 132에 대해 확인해보자.
120 + 110 + 132 + 132 = 494로 배분이 불가능하다. 따라서 최댓값은 113 이상 132 미만이다.
그러면 이번에는 114와 131 사이의 값인 122에 대해 확인해보자.
120 + 110 + 122 + 122 = 474로 배분이 가능하다. 따라서 최댓값은 113 이상 132 미만이다.
…
이 과정을 반복하다 보면 127이상 129미만이라는 사실을 알 수 있다.
이렇게 되면 마지막으로 남은 범위는 128이므로, 128에 대해 확인을 해 보면 분배가 불가능하다는 사실을 알 수 있다. 따라서 127이 최대 예산임을 알 수 있다.
그러면 이 과정을 코드로 표현해보자.
최솟값을 l, 최댓값을 r로 표현한다.
두 값의 평균이 조건을 만족하면 최솟값을 평균 + 1,
조건을 만족하지 않으면 최댓값을 평균 - 1로 갱신한다.
그리고 최솟값이 최댓값을 넘어가면 끝낸다.
solution_search.cpp
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<int> budgets, int M) {
int l = 1, r = *max_element(budgets.begin(), budgets.end());
while (l <= r)
{
int m = (l + r) / 2;
long long sum = 0;
for (int v : budgets)
sum += static_cast<long long>(min(v, m));
if (sum <= static_cast<long long>(M)) l = m + 1;
else r = m - 1;
}
return l-1;
}
프로그래머스의 남은 이분 탐색 문제도 이 방법을 응용하면 풀 수 있는 문제들이다. 다른 문제에서도 이 방법을 응용해서 풀어보자.

Comments