프로그래머스 - 순위

https://programmers.co.kr/learn/courses/30/lessons/49191

 

문제 설명

n명의 권투선수가 참가한 대회가 있다.
경기는 1 vs 1로 진행하며, 만약 A 선수가 B 선수보다 실력이 좋으면 A 선수는 B 선수를 항상 이긴다.
주어진 경기 결과를 토대로 선수들의 순위를 매기려고 했으나, 경기 결과의 일부분을 잃어버렸다.

선수의 수와 경기 결과를 담은 배열을 토대로, 정확하게 순위를 매길 수 있는 선수의 수를 리턴하자.

 

제한 사항

• 1 <= 선수의 수 <= 100
• 1 <= 경기 결과 <= 4,500
• 각 배열의 요소 [A, B]는 A 선수가 B 선수를 이겼다는 것을 의미이다.
• 모순되는 경기 결과는 없다.

 

1. 그래프 탐색 - O(N^2)

 

문제의 내용 중에는 다음과 같은 내용이 있다.

A 선수가 B 선수보다 실력이 좋으면, A 선수는 B 선수를 반드시 이긴다.

그렇다면 다음의 문장도 성립할 수 있을 것이다.

B 선수가 C 선수를 이긴다면, A 선수는 C 선수를 이긴다.
A 선수가 D 선수에게 진다면, B 선수도 D 선수에게 진다.

현실에서야 언더독의 반란같은 것이 일어날 수도 있으나, 안타깝게도 이 문제의 세계에서는 그런건 없는 것 같다.

즉, 각 선수들에겐 보이지 않는 무언가의 능력치가 있어서, 두 선수간의 능력치가 큰 쪽이 무조건 이기는 방식이라고 보면 된다.

따라서, 풀 리그로 경기를 치루게 된다면 순위는 무조건 이런 결과가 나올 것이다.

 

---

n명의 권투선수가 있으면,

1등은 n-1승 0패다.
2등은 n-2승 1패다.
3등은 n-3승 2패다.

…

꼴등은 0승 n-1패다.

---

 

그러면 주어진 예시를 보면서 생각해보자.

[[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]]

그러면 1번 선수부터 순위를 매길 수 있는지 확인해보자.

1번 선수가 이기는 상대를 찾아보자.
결과표 상으로 이기는 상대는 2번이 있다. 그리고 2번은 5번에게 이긴다.
따라서, 1번이 이기는 상대는 2번과 5번으로, 최소 2승은 한다는 사실을 알 수 있다.

그러면 1번이 지는 상대는 누구일까?
결과표 상으로 지는 상대는 보이지 않는다.
2번을 이기는 상대들은 여럿 있으나, 그들이 1번을 이긴다는 보장은 없다.
따라서 1번이 누구에게 지는지는 알 수 없다.

따라서 1번은 2번과 5번에게 이긴다는 사실만 알 수 있으므로, 순위를 확정할 수 없다.

그러면 2번의 순위를 매겨보자.

2번이 이기는 상대는 위에서 확인했듯이, 5번 하나 뿐이다.
2번이 지는 상대들은 4번, 3번, 그리고 1번이다.
따라서 확인할 수 있는 전적은 1승 3패이다.

위의 순위표를 다시 한번 살펴보자. 1승 3패면 몇등일까?
총 선수는 5명이므로, 1등은 4승 0패가 될 것이고, 꼴등은 0승 4패가 될 것이다. 그리고 꼴등보다 1승을 더 하면 1승 3패로, 꼴등바로 윗순위, 즉 4등이 될 것이다.

따라서 2번은 4등임을 확신할 수 있다.

3번과 4번에 대해서도 위와 같은 순서를 거치면, 확실히 알 수 있는 성적이 각각 2승 1패, 그리고 3승 0패 라는 것을 알 수 있다. 둘 다 1번 선수와의 승/패를 알 수 없기 때문에, 순위를 확정할 수 없다.

그러면 5번 선수는 어떨까?

5번 선수가 이기는 경기 결과는 찾아볼 수 없다. 따라서 최소 0승이다.
그리고 5번 선수가 지는 경기 결과는 딱 하나 찾을 수 있다. 바로 2번 과의 경기 결과다.
2번은 누구에게 졌는가? 1,3,4번에게 졌다.
그렇다는 것은 5번도 1,3,4번에게 진다는 것을 의미한다.

따라서 확인할 수 있는 5번의 전적은 0승 4패가 된다. 그리고 이는 곧 꼴등을 의미한다.

 

등수를 확정할 수 있는 2번과 5번을 한 번 보자.
2등은 확정할 수 있는 승/패가 1승 3패다. 합하면 4가 된다.
5등은 확정할 수 있는 승/패가 0승 4패다. 합하면 4가 된다.

즉, 확정할 수 있는 승/패를 합한 값이 n-1이 되면, 등수를 확정할 수 있다. 위의 등수를 나열한 텍스트를 확인해도, 승과 패를 더하면 n-1이 된다는 점을 확인할 수 있다.

그러면 이것을 어떻게 확인할까? 선수 i가 있다고 치자.

i 선수가 이긴 선수들에 대해, 이 선수들이 이긴 상대가 얼마나 되는지 알아보자.
그리고 i선수가 진 선수들에 대해, 이 선수들이 진 상대가 얼마나 되는지 알아보자.
이 두 값의 합이 n-1이 된다면, 선수 i의 순위를 확정할 수 있다.

하지만 그렇다고 무작정 결과 표를 계속해서 순회하자니, 시간이 어마어마하게 걸릴 것 같다.

이럴 때, 선수간의 관계를 그래프로 표현하여 승/패를 표현할 수 있다.

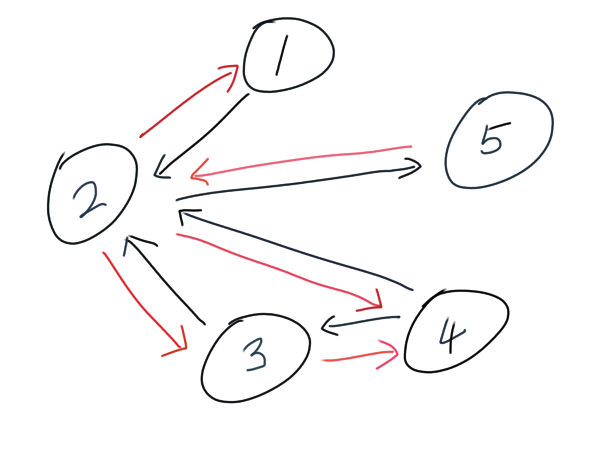
위의 그림처럼 경기 결과에 따라 그래프를 구성해보자. A가 B를 이겼다면, A -> B 의 간선은 검은 색으로, B -> A의 간선은 빨간 색으로 정해주자. 물론 코드가 검은 색/빨간 색을 구분할 수는 없으니, 두 간선의 값에 차이를 주는 것 만으로도 충분하다.

그래프를 완성했으면, 모든 선수들에 대하여 이긴 선수/진 선수에 대해 순회를 시작해보자.

이기는 선수에 대해 알아볼 때, 계속해서 검은 선을 따라가면서 방문한 수를 확인하고, 지는 선수에 대해 알아볼 때, 계속해서 빨간 선을 따라가면서 방문한 수를 확인하자.

그리고 선수 간의 관계를 따라가다 보면, 이미 확인 했던 선수를 다시 확인하는 경우도 발생할 수 있다. 중복 방문에 대한 대책도 세워두자.

그리고 순회한 선수의 총 수를 합한 뒤, 합이 n-1이라면 순위를 확정할 수 있는 선수이므로 순위를 확인 가능한 선수 숫자에 1을 더해주자.

이런 식으로 모든 선수에 대해 그래프 순회를 한다면, 문제의 답을 구할 수 있다.

그럼 위의 내용을 코드로 표현해보자.

 

solution.cpp

#include <vector>

using namespace std;

void dfs(vector<vector<int>>& g, vector<bool>& dirt, int idx, int val)
{
    dirt[idx] = true;
    
    for (int i=0;i<g.size();++i)
        if (!dirt[i] && g[idx][i] == val)
            dfs(g, dirt, i, val);
}

int search(vector<vector<int>>& g, int idx)
{
    vector<bool> dirt(g.size(), false);
    dirt[idx] = true;
    
    for (int v = -1; v<3; v += 2)
    {
        for (int i=0;i<g.size();++i)
        {
            if (!dirt[i] && (g[idx][i] == v))
                dfs(g,dirt,i,v);
        }
    }
    int result = 0;
    for (bool b : dirt)
        result += b;
    
    return result;
}

int solution(int n, vector<vector<int>> results) {
    vector<vector<int>> g(n, vector<int>(n,0));
    
    for (vector<int> vi : results)
    {
        g[vi[0]-1][vi[1]-1] = 1;
        g[vi[1]-1][vi[0]-1] = -1;
    }
    
    int answer = 0;
    for (int i=0;i<n;++i)
        if (search(g, i) == n)
            ++answer;
    
    return answer;
}