프로그래머스 - 단속카메라

https://programmers.co.kr/learn/courses/30/lessons/42884

 

문제 설명

고속도로를 이동하는 차량들이 있다.
이 차량들을 한 번은 만나도록 단속용 카메라를 설치하고자 한다..

고속도로를 이동하는 차량의 경로 routes 배열을 토대로, 모든 차량이 단속용 카메라에 만날 수 있도록 하기 위한 최소 단속 카메라의 수를 리턴하자.

 

제한 사항

• 1 <= 차량의 대수(N) <= 10,000
• routes[0] : 진입지점, routes[1] : 나가는 지점
• 진입/진출 지점에 설치되어 있어도 카메라를 만난 것으로 간주한다.
• -30,000 <= 진입/진출 지점 <= 30,000

 

1. 정렬 후 탐색 - O(NlogN)

단속 카메라의 수를 최소한으로 만드려면 어떻게 해야 할까?
가능한 많은 차량이 공통적으로 지나는 곳에 카메라를 설치하면 하나의 카메라로 많은 차량을 단속할 수 있을 것이고, 이는 설치해야 할 카메라의 수를 줄여주는 효과를 얻을 수 있을 것이다.

그러면 공통적으로 지나는 장소는 어떻게 찾아야 할까?

주어진 예시를 한 번 살펴보자.

[[-20,15], [-14,-5], [-18,-13], [-5,-3]]

글자만으로는 잘 감이 오지 않는다. 한 번 그림으로 그려보자.

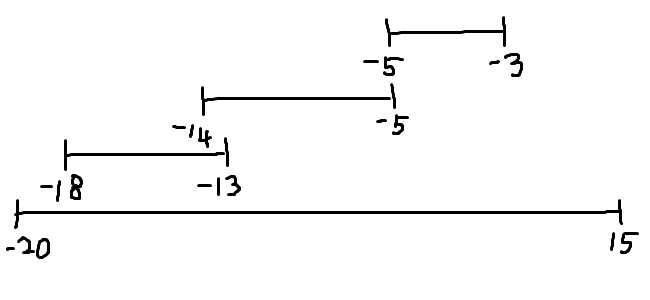-3과 15의 거리가 너무 짧아보이는건 신경쓰지 말자.

가장 눈에 띄는건 [-20, 15] 를 지나는 차량이다.
가장 먼저 진입해서, 가장 먼저 나간다. 모든 차량과의 경로와 겹치고 있다.

그럼 그 다음으로 먼저 진입하는 차량인 [-18, -13]을 보자. [-20, 15]와 비교하면 상당히 짧은 구간을 이동한다.
그러면 [-20, 15]와 [-18, -13]의 공통구간은 어떻게 될까? [-20, 15]안에 [-18, -13]이 있는 그림이므로, 공통되는 구간은 [-18, -13]이 된다.

그럼 그 다음으로 먼저 진입하는 차량인 [-14, -5]를 살펴보자.
지금까지의 공통구간 [-18, -13]과 [-14, -5]의 공통구간은 어떻게 될까? 그림을 통해 알 수 있지만, [-14, -13]이 공통구간이 된다. 따라서, 지금까지의 이 3개의 차량을 하나의 카메라로 단속하기 위해서는 -14 또는 -13에 설치해야 한다는 의미이다.

그럼 마지막으로 남은 차량인 [-5,-3]을 살펴보자.
지금까지의 공통구간 [-14, -13]과 [-5, -3]의 공통구간은 어떻게 될까?
없다. 너무나도 멀리 떨어져있다. 이 이상은 겹칠 수 없다. 따라서, [-5,-3]도 같이 단속하기 위해서는 어쩔 수 없이 단속카메라를 하나 더 들여야 한다. 그러면 2번째 단속카메라는 어디에 둬야 할까?
그냥 [-5, -3]구간 중 아무데나 두면 된다. [-14, -5] 차량과 [-5,-3] 차량이 겹치는 구간인 -5에 둬야 할 것 같은 느낌이 들기도 하지만, [-14,-5]차량은 이미 [-14,-13]구역에 설치된 카메라로 단속하고 있다. 굳이 한번 더 단속을 할 필요는 없다.

따라서 총 필요한 카메라의 최솟값은 2가 된다.

위의 과정을 글로 표현하면 다음과 같다.

• 가장 먼저 진입하는 차량부터 차례대로 살펴본다.
• 현재 살펴보고 있는 공통 구간과 살펴보는 차량과의 공통구간이 있다면, 공통구간을 갱신해준다.
• 만일 더 이상 공통구간이 없다면, 설치해야 하는 카메라 수를 1 늘이고, 현재 살펴보고 있는 차량의 구간을 공통 구간으로 갱신한다.

 

이제 위의 내용을 코드로 표현해야 한다. 어떻게 해야 할까?

가장 먼저 진입하는 차량부터 살펴보고 싶으므로, 정렬을 하는 것이 좋겠다. routes[i][0]에 대해 오름차순으로 정렬하자.

이 문제에서는 routes[i][0]이 routes[i][1]보다 항상 작거나 같다는 조건은 없으나, 테스트케이스 상으로는 그렇게 주어지는 것으로 보인다. 만약 좀 더 확실하게 하고 싶다면, 모든 routes[i]에 대해 routes[i][0]이 routes[i][1]보다 크다면, swap을 해 주는 코드를 포함하는 것이 좋다.

정렬이 되었다면, 가장 먼저 진입한 차량부터 차근차근 살펴보자.

 

현재까지의 공통구간의 시작점을 begin, 끝점을 end라고 치자.
새로 들어온 차량 routes[i]와 현재까지의 공통구간이 겹치는 여부는 어떻게 해야 알 수 있을까?

routes[i][0], 즉 차량의 시작 지점이 현재까지의 공통구간 end보다 크면 겹치는 구간이 없고, 작거나 같으면 공통구간이 있다는 것을 알 수 있다. routes[i][1]은 routes[i][0]보다 크거나 같고, end는 begin보다 크거나 같기 때문이다.

만약 routes[i][0]이 end보다 크다면, 더 이상의 공통구간은 없으므로, 설치해야 하는 카메라 수를 1 늘이고, begin은 routes[i][0]으로, 그리고 end는 routes[i][1]로 갱신하면 된다.

만약 routes[i][0]이 end보다 작거나 같다면, 아직은 공통구간이 존재한다는 의미이므로, begin은 지금의 begin과 routes[i][0]중 큰 쪽으로, 그리고 end는 지금의 end와 routes[i][1]중 작은 쪽으로 골라야 공통구간이 될 것이다.

여기서 하나 생각해보자. begin이 routes[i][0]보다 커질 일이 있을까? 우리는 routes 배열을 routes[i][0]을 기준으로 오름차순으로 정렬했다. 즉, begin은 routes[j][0] (j는 i보다 작은 값)이므로, begin이 자기 자신의 값을 유지할 일은 절대로 없다.
따라서, begin의 값은 무조건 routes[i][0]의 값으로 갱신된다.

그리고 하나 더 생각해보자. 겹치는 구간을 계산할 때, begin을 사용했었는가? 전혀 사용하지 않았다. end와 routes[i][0]만을 비교하고 있었다. 따라서, begin변수는 없어도 된다. end 변수만 잘 유지하면 답을 구할 수 있다는 것을 의미한다.

 

그러면 아까 적었던 내용 중, 필요없는 내용은 삭제하자.

만약 routes[i][0]이 end보다 크다면, 더 이상의 공통구간은 없으므로, 설치해야 하는 카메라 수를 1 늘이고, begin은 routes[i][0]으로, 그리고 end는 routes[i][1]로 갱신하면 된다.

만약 routes[i][0]이 end보다 작거나 같다면, 아직은 공통구간이 존재한다는 의미이므로, begin은 지금의 begin과 routes[i][0]중 큰 쪽으로, 그리고 end는 지금의 end와 routes[i][1]중 작은 쪽으로 골라야 공통구간이 될 것이다.

 

그럼 위의 내용을 코드로 표현해보자.

 

solution.cpp

#include <vector>
#include <algorithm>

using namespace std;

int solution(vector<vector<int>> routes) {
    int answer = 1;
    sort(routes.begin(), routes.end());
    int r = routes[0][1];
    
    for (int i=1;i<routes.size();++i)
    {
        if (routes[i][0] > r)
        {
            ++answer;
            r = routes[i][1];
        }
        else    r = min(r, routes[i][1]);        
    }
    
    return answer;
}