프로그래머스 - 네트워크

https://programmers.co.kr/learn/courses/30/lessons/43162

 

문제 설명

네트워크란 컴퓨터 간에 정보를 교환할 수 있도록 연결된 형태를 의미한다. A와 B가 연결되어 있고, B와 C가 연결되어 있다면, A와 C는 B를 통해 정보를 교환할 수 있기 때문에 하나의 네트워크 상에 있다고 할 수 있다.

컴퓨터의 개수와 연결 정보를 토대로, 네트워크의 개수를 리턴하자.

 

제한 사항

• 1 <= 컴퓨터의 개수 <= 200
• 각 컴퓨터는 0부터 컴퓨터의 개수 - 1인 정수로 표현한다.
• i와 j가 연결되어 있을 경우, 배열[i][j]는 1이고, 연결되어 있지 않을 경우 0이다.
• 배열[i][i]는 항상 1이다.

 

1. DFS/BFS - O(N^2)

문제 상의 예제를 보면 알 수 있듯이, 하나로 묶인 네트워크가 총 몇개가 있는지 물어보는 문제이다. 이를 알아보는 방법은 간단하다. 모든 컴퓨터에 대해, 자신과 연결된 컴퓨터에 대해 모두 탐색을 해 보면 되는 일이다.

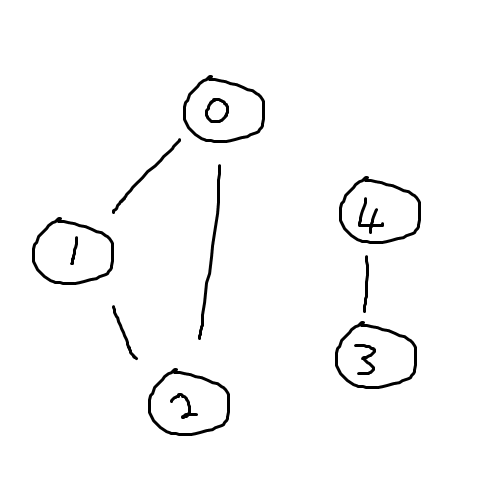
위와 같이 네트워크가 주어졌다고 생각해보자.
아무데서나 시작해도 괜찮지만, 가장 숫자가 낮은 0번부터 시작해보자.
그리고 방문한 곳의 컴퓨터에는 방문했다는 흔적을 남겨두자.

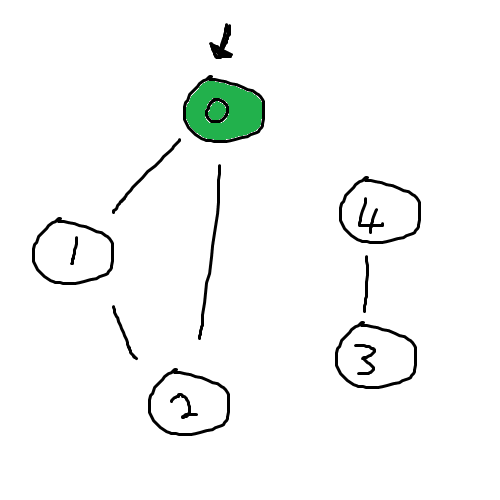
0번 컴퓨터에서 갈 수 있는 곳은 1번과 2번이다.
여기서 아무데나 가도 괜찮다. 여기서는 1번으로 가 보자.
1번으로 이동한 뒤, 방문했다는 흔적을 남겨두자.

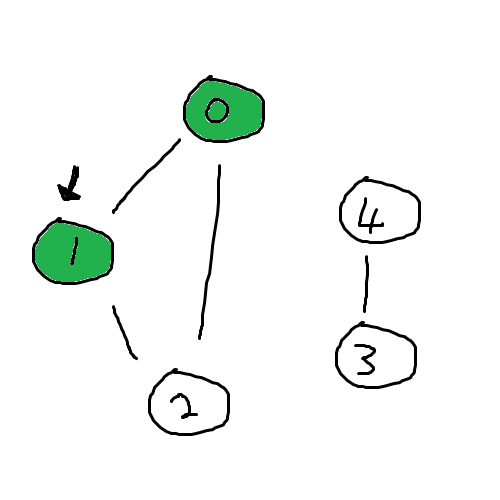
1번 컴퓨터에서 갈 수 있는 곳은 0번과 2번이다.
0번을 확인해보니, 이미 방문한 흔적이 있다. 따라서 또 갈 필요는 없다.
그러면 남은 컴퓨터 2번을 방문해보자.

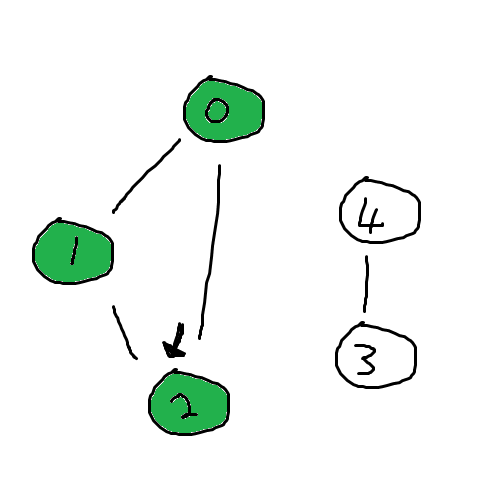
2번에 와 보니, 갈 수 있는 곳 0번과 1번 모두 이미 방문한 흔적이 있다. 이제 여기서는 더 이상 갈 수 있는 곳이 없다. 따라서 0,1,2가 하나의 네트워크로 이루어져 있음을 알 수 있다.

그리고 나머지 3,4도 동일한 과정을 거치면 총 네트워크는 2개가 됨을 알 수 있다.

 

현재 탐색하는 컴퓨터가 들릴 수 있는 곳을 모두 들려보면서, 흔적 잘 남겨서 중복탐색을 막으면 된다는 사실을 알았다.

이 과정에서 깊이 우선 탐색(DFS)나 너비 우선 탐색(BFS)를 사용할 수 있는데, 이 문제에서는 아무거나 써도 답을 구하는데 지장이 없다.

그러면 우선 DFS로 문제를 풀어보자.

 

solution_dfs.cpp

#include <vector>

using namespace std;

void dfs(int v, int n, vector<vector<int>>& computers, vector<bool>& dirt)
{
    dirt[v] = true;
    
    for (int i=0;i<n;++i)
        if (computers[v][i] && !dirt[i])
            dfs(i, n, computers, dirt);
}

int solution(int n, vector<vector<int>> computers) {
    int answer = 0;
    vector<bool> dirt(n, false);
    
    for (int i=0;i<n;++i)
    {
        if (!dirt[i])
        {
            dfs(i, n, computers, dirt);
            ++answer;
        }
    }
    
    return answer;
}

 

그러면 이번에는 BFS를 사용해보자.

 

solution_bfs.cpp

#include <vector>
#include <queue>

using namespace std;

int solution(int n, vector<vector<int>> computers) {
    int answer = 0;
    queue<int> qu;
    vector<bool> dirt(n, false);
    
    for (int i=0;i<n;++i)
    {
        if (dirt[i])    continue;
        
        qu.push(i);
        ++answer;
        
        while (!qu.empty())
        {
            dirt[qu.front()] = true;
            
            for (int j=0; j<n; ++j)
                if (computers[qu.front()][j] && !dirt[j])
                    qu.push(j);
            
            qu.pop();
        }
    }
    
    return answer;
}

 

2. Union-Find(Disjoint Set) - O(N^2)

이번에는 조금 특별한 방법으로 풀어보자.

Union-Find 알고리즘이란 것이 있다.
말 그대로 두 원소에 대해
Union - 하나의 집합으로 묶어주고
Find - 같은 집합에 있는지 찾아준다.

컴퓨터 0과 1이 연결되어 있으면 Union으로 하나의 집합으로 묶어주고, 1과 2가 연결되어 있으면 Union으로 하나의 집합으로 묶어준다. 이 떄, 0과 2도 하나의 집합이 된다.

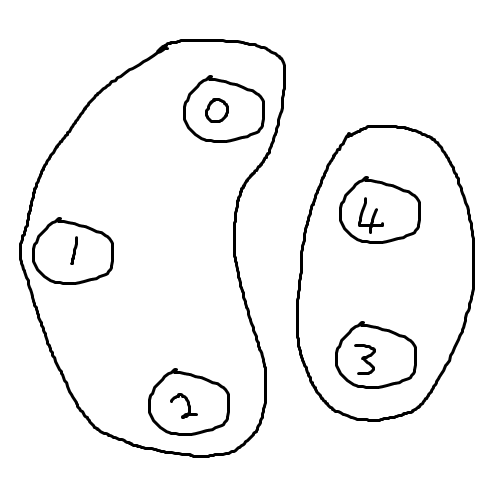
어떻게 하면 위와 같이 하나의 집합으로 표현할 수 있을까?
DFS에서 사용했던 예제를 Union-Find에 적용해보자.

 

처음에는 각자 자신 하나만이 포함되어 있는 집합으로 표현한다.
이 집합의 번호는 자신의 숫자로 표현하자.

0	1	2	3	4
0	1	2	3	4

0과 1은 연결되어 있으므로, 하나의 집합이라 볼 수 있다.
그러면 0과 1을 Union, 즉 합쳐야 한다. 그런데 어떻게 해서 합쳤다는 것을 표현할까?

0의 집합번호와 1의 집합번호를 똑같이 만들어주면 된다.
그러면 누가 번호를 바꿀 것인가도 생각을 해야 한다.
기준은 정하기 나름이다. 숫자가 작은 쪽이 큰 쪽의 번호로 바꾸든, 숫자가 큰 쪽이 작은 쪽으로 번호를 바꾸든, 일관된 규칙을 정하면 된다. 여기서는 숫자가 큰 쪽이 작은 쪽으로 바꾸는 방식을 선택하자. 이 떄, 번호를 유지하는 쪽을 부모로 취급한다. 그러면 집합의 번호는 다음과 같이 될 것이다.

0	1	2	3	4
0	0	2	3	4

1과 2도 연결되어 있으므로, 하나의 집합이라 볼 수 있다.
그러면 1과 2를 Union, 즉 합쳐야 한다.
그러면 이번엔 합치는 표현을 어떻게 해야 할까?

1의 집합 번호는 0이고, 2의 집합 번호는 2니, 2의 집합번호를 0으로 바꾸면 되지 않을까? 라는 생각을 할 수 있다.

결과적으로는 맞다. 다만 과정은 좀 생각을 해 봐야 한다. 이 과정에 대해서는 잠시 후에 다뤄보기로 하고, 지금은 넘어가자.

0	1	2	3	4
0	0	0	3	4

그리고 3과 4에 대해서도 동일한 동작을 해 주면, 결과적으로는 다음과 같은 집합을 가지게 될 것이다.

0	1	2	3	4
0	0	0	3	3

집합의 종류가 몇 가지인지는 어떻게 확인할까?
위의 집합 표 상에 존재하는 숫자의 종류는 0과 3이다. 따라서 2종류의 집합이 있다는 것을 알 수 있고, 실제로 같은 집합 번호를 가진 컴퓨터 끼리는 실제로 연결되어 있는 컴퓨터들이다. 따라서 정답 2를 리턴하면 된다.

 

그러면 위의 병합 과정에서 무엇이 부족했던 것인가?

지금까지의 병합 과정이 다음과 같이 이루어졌다고 가정해보자.

0	1	2	3	4
0	0	0	3	3

그리고 새롭게 2와 4의 연결이 생겼다고 가정해보자. 그러면 2와 4도 하나의 집합이란 사실을 알게 되고, 모든 컴퓨터는 하나의 네트워크 안에 존재한다는 사실을 알게 된다.

그러면 아까처럼 단순히 집합 번호를 옮기면 어떻게 될까?

0	1	2	3	4
0	0	0	3	0

4번 컴퓨터의 집합 번호가 0이 되었다. 하지만 3번은 그대로다. 모두가 하나가 되어야 하는데, 3번은 여전히 본인의 집합 번호인 3번을 유지하고 있다.
따라서 단순히 i와 j가 병합을 했다고 i와 j의 집합 번호를 바꾸면 안된다는 사실을 알았다. 그러면 어떻게 해야 할까?

 

간단하다. 2의 집합의 최고 부모와 4의 집합의 최고 부모의 값을 변경하면 된다. 2의 최고부모는 0이고, 4의 최고 부모는 3이다. 3의 집합 번호가 더 작으므로, 3의 집합번호를 0으로 바꾸면 된다.

이러면 4는 여전히 집합 번호가 3이긴 하지만, 3의 집합번호 0을 보고, 자신의 집합번호가 0임을 확인할 수 있다. 위와 같이 탐색중인 번호와 실제 집합번호가 일치할 때 까지 찾아가는 과정이 바로 Find 함수가 수행하는 일이다.
모든 Union과정을 거친 후, 실제 집합의 개수를 셀 때도 각자의 원소에 대해 Find 함수의 결과값을 토대로 실제 집합의 개수를 세어야 한다.

그러면 이 과정을 코드로 표현해보자.

 

solution_union.cpp

#include <vector>
#include <unordered_set>

using namespace std;

int findG(vector<int>& g, int v)
{
    while (g[v] != g[g[v]])   v = g[v];
    return g[v];
}

int solution(int n, vector<vector<int>> computers) {
    vector<int> g(n,0);
    for (int i=1;i<n;++i)   g[i] = i;
    
    for (int i=0;i<n;++i)
    {
        for (int j=i+1;j<n;++j)
        {
            if (computers[i][j])
            {
                int l = findG(g, i);
                int r = findG(g, j);
                g[max(l,r)] = min(l,r);
            }
        }
    }
    
    unordered_set<int> st;
    for (int v : g)
        st.insert(findG(g,v));
    return st.size();
}

 

사실 이 문제는 굳이 Union-Find를 사용할 필요가 없는 문제이다. 하지만 알아두면 써먹을 데가 은근히 있을 것이다.